Kasus 2 Plat Sejajar dengan Grid Dependeny Test

Ketika suatu fluida mengalir pada sebuah pipa, maka dianggap bahwa fluida mengalir pada dua plat sejajar. Kita dapat melihat bagaimana fenomena kecepatan fluida tersebut ketika mengalir diantara dua plat sejajar tersebut. Distribusi kecepatan aliran fluida ternyata tidaklah sama. Untuk melihat fenomena aliran fluida tersebut,maka berikut akan dilakukan simulasi CFD pada kasus berikut :

      Dari gambar di atas, terdapat dua plat yang sejajar dengan jarak H=0,2 m  dan dengan panjang L=1m, lalu dialirkan udara (laminar) dengan densitas rho=1,2 kg/m³.

Terdapat 2 Kasus yang terdapat dalam contoh ini .Yaitu dengan mengganti salah satu parameter :

1.      Mengganti viskositas m = 4x10^-5 kg/m.s dan m = 10^-5 kg/m.s dengan menetapkan kecepatan inlet u _inlet = 0,01m/s

2.      Mengganti kecepatan inlet u _inlet = 0,01 m/s dan u _inlet= 0,04 m/s dengan menetapkan viskositas m = 4x10^-5  kg/m.s

 
Cari dan analisis dengan menggunakan CFDSOF untuk kedua kasus diatas

Berikut langkah-langkah untuk melakukan simulasi dengan menggunakan CFDSOF

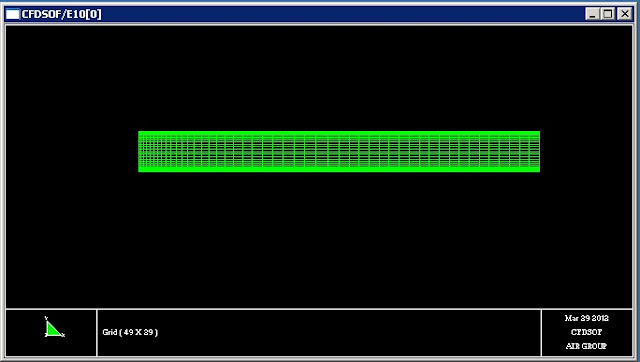
1.      Masukkan parameter awal yaitu panjang  1 m dan tinggi 0.1 m dengan jumlah cell 50 x 30.  Kemudian lakukan perbedaan grid untuk daerah masuk fluida, dengan melakukan perbedaan grid sehingga mengakibatkan terjadinya kerapatan atau rasio antar cell menjadi kecil dan hal ini sangat berguna untuk memudahkan kita  melihat fenomena yang terjadi didaerah tersebut. Pada kasus kali ini, grid yang terbentuk akan dibedakan yaitu dengan memberikan faktor pemberat  pada titik mulai dan titik akhir pada saat proses modif segmen.

2.      Lakukan pembagian segemen terhadap arah x dan y. Untuk daerah arah x dibagi atas 2 segmen dimana terdiri dari 28 dan 20 cell. Dan titik awal segmen 1  dengan titik sumbu x ( 0,0 ) ,titik awal  segmen 2  dengan titik sumbu x ( 0.5,0 ) dan titik akhir segmen 2 dengan titik sumbu x ( 1,0 ) . Sedangkan untuk daerah y dibagi atas 3 segmen dimana terdiri dari 10,8 dan 10 cell. Dan titik awal segmen 1 dengan titik sumbu y ( 0,0 ), titik awal segmen 2 dengan titik sumbu y ( 0,0.025 ), titik awal segmen 3 dengan titik sumbu y ( 0, 0.075 ) dan titik akhir segmen 3 dengan titik sumbu y ( 0, 0.1 )

 

3.      Pada cell yang telah dibuat, diberikan inlet 1 dan inlet 2. Dengan inlet 1 diberikan kecepatan udara dan inlet 2 diberikan tekanan 0 Pa.

4.      Masukkan nilai konstanta fisikal berupa nilai density fluida= 1.2 dan viskositas fluida= 4 x 10^-5 kg/m². Masukkan nilai konstanta sempadan berupa kecepatan fluida 0.01 m/s (untuk kasus 1)

5.      Iterasi sampai nilainya konvergen dan lihat gambar kontur kecepatan serta plot X-Y

6.      Untuk kasus 2 ulangi langkah 4 dengan density dan kecepatan fluida tetap sedangkan yang di ubah hanya viskositas 1 x 10^-5 kg/m². Iterasi sampai nilainya konvergen dan lihat gambar kontur kecepatan serta plot X-Y

7.      Untuk kasus 3 ulangi langkah 3 dengan  density tetap dan kecepatan fluida 0.04 m/s dan viskositas 4 x 10^-5 kg/m². Iterasi sampai nilainya konvergen dan lihat gambar kontur kecepatan serta plot X-Y

Hasil Simulasi yang dihasilkan
Kasus 1 ku = 0.01 m/s dengan viskositas 4 x 10^-5

Kasus 2 ku = 0.01 m/s dengan viskositas 1 x 10^-5

Kasus 3 ku = 0.04 m/s dengan viskositas 4 x 10^-5

      Untuk kasus 1 dan kasus 2 dengan parameter kecepatan fluida konstan/tetap dan di variasikan nilai dari viskositas absolut fluida dinamis, maka dari persamaan rumus reynold dengan bertambahnya nilai viskositas maka nilai bilangan reynold yang dihasilkan akan semakin kecil. Dengan nilai dari bilangan Reynold yang semakin kecil maka aliran yang terbentuk menjadi laminar. Semakin laminar suatu aliran maka distribusi alirannya menjadi mudah seragam sehinggga etrance regionnya menjadi kecil dan Fully developed flow cepat terbentuk. Nah sebaliknya dengan rendahnya nilai viskositas maka bilangan reynold yang dihasilkan akan semain besar. Yang mengakibatkan aliran menjadi turbulen, dengan aliran yang turbulence mengakibatkan gerakan molekur yang semakin acak sehingga untuk menjadi mengakibatkan entrance regionnya semakin lama dan Fully developed flownya semakin lama.

        Untuk Kasus 1 dan kasus 3 dengan parameter kecepatan fuida yang di variasikan dan viskositas absolut fluida dinamis yang dijaga tetap atau konstan. Makin besar kecepatan fluida yang diberikan maka bilangan Reynold yang dihasilkan akan semakin besar sehingga terbentuknya aliran turbulen semakin mudah sehingga untuk mencapai Fully Developed Flow akan semakin lama. Sebaliknya dengan semakin rendah kecepatan fluida maka bilangan Reynold yang dihasilkan semakin rendah sehingga mudahnya terbentuknya aliran laminar dan Fully Developed Flow semakin mudah dan entrance Regionnya semakin kecil.